
1. Tổng Quan và Định Hướng Chương Trình
Phần mở đầu của tài liệu giới thiệu rõ ràng về mô hình tổng quát, mục tiêu, và phương pháp tiếp cận của môn học, đặt nền tảng cho toàn bộ quá trình học tập.
1.1. Mô hình Tổng Quát và Mục Tiêu
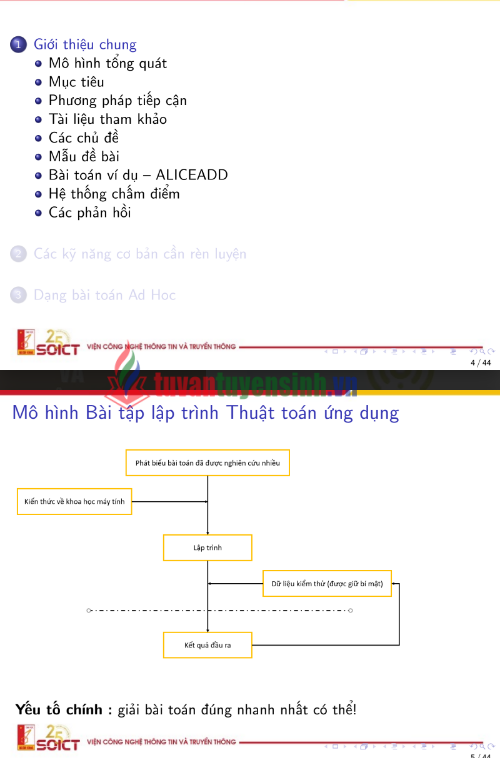
Mô hình tổng quát của bài tập lập trình thuật toán, như được hình dung trong slide, là sự kết hợp chặt chẽ giữa Tư Duy Thuật Toán và CTDL với Kỹ Năng Lập Trình . Điều này ngụ ý rằng, việc nắm vững cú pháp lập trình chỉ là điều kiện cần; điều kiện đủ và quan trọng hơn là khả năng phân tích bài toán, lựa chọn cấu trúc dữ liệu tối ưu, và thiết kế thuật toán hiệu quả.
Mục tiêu của chương trình không chỉ dừng lại ở việc người học hiểu các thuật toán cổ điển, mà còn phải biết ứng dụng chúng vào các bài toán thực tế. Mục tiêu cốt lõi là xây dựng được tư duy giải quyết vấn đề (problem-solving mindset) trong môi trường lập trình. Người học cần phải:
- Hiểu sâu sắc về các thuật toán và CTDL cơ bản.
- Có khả năng phân tích độ phức tạp thời gian và không gian của thuật toán.
- Phát triển kỹ năng triển khai các ý tưởng thuật toán thành mã nguồn chính xác và tối ưu.
1.2. Phương pháp Tiếp Cận và Nội dung
Tài liệu giới thiệu phương pháp tiếp cận bao gồm việc nghiên cứu các chủ đề thuật toán khác nhau, đi kèm với các mẫu đề bài và bài toán ví dụ cụ thể (như bài toán ALICEADD). Điều này cho thấy tính ứng dụng cao và sự kết hợp giữa lý thuyết và thực hành được đề cao.
Các chủ đề được trình bày một cách đa dạng, trải dài từ các vấn đề cơ bản đến nâng cao, đảm bảo người học có cái nhìn toàn diện:
- Các thuật toán cơ bản (ví dụ: Tìm kiếm, Sắp xếp).
- Các cấu trúc dữ liệu cơ bản (ví dụ: Danh sách, Cây, Đồ thị).
- Các kỹ thuật giải thuật (ví dụ: Quy hoạch động, Tham lam, Quay lui).
- Các dạng bài toán Ad Hoc và xử lý chuỗi.
- Các phương pháp giải bài toán NP-khó.
Sự tồn tại của Hệ thống chấm điểm (Judging System) trong mô hình tổng quát là một điểm rất thực tế, phản ánh môi trường thi đấu lập trình (Competitive Programming) hoặc môi trường làm việc thực tế, nơi mã nguồn phải được kiểm tra tự động về tính đúng đắn và hiệu suất.
2. Các Kỹ Năng Cơ Bản Cần Rèn Luyện
Phần này là trọng tâm của tài liệu, liệt kê các kỹ năng bắt buộc phải thành thạo, không chỉ trong học tập mà còn trong sự nghiệp phát triển phần mềm. Việc liệt kê các kỹ năng này cho thấy sự chuyên nghiệp và định hướng thực tế của tài liệu.
2.1. Kỹ năng Phân Tích Bài Toán
Trước khi viết bất kỳ dòng mã nào, kỹ năng quan trọng nhất là phân tích đầu vào (Input) và đầu ra (Output), cùng với việc xác định các ràng buộc (Constraints) của bài toán.
- Đầu vào: Cần xác định rõ định dạng, kiểu dữ liệu, và số lượng của dữ liệu đầu vào.
- Ràng buộc: Các ràng buộc về kích thước dữ liệu (ví dụ: $N \le 10^5$), thời gian xử lý (ví dụ: dưới 1 giây), và bộ nhớ là yếu tố quyết định để chọn thuật toán phù hợp. Nếu không tính toán được độ phức tạp thời gian, việc chọn thuật toán có thể dẫn đến Time Limit Exceeded (TLE), một lỗi phổ biến trong lập trình thuật toán.
2.2. Kỹ năng Triển khai Thuật Toán
Đây là bước chuyển đổi từ ý tưởng lý thuyết sang mã nguồn thực thi. Kỹ năng này đòi hỏi sự hiểu biết sâu sắc về các cú pháp ngôn ngữ lập trình và cách sử dụng CTDL.
- Lựa chọn CTDL: Việc lựa chọn đúng cấu trúc dữ liệu (ví dụ: dùng HashMap thay vì duyệt List để tìm kiếm) có thể giảm độ phức tạp từ $O(N)$ xuống $O(1)$, mang lại hiệu suất vượt trội.
- Chiến lược Coding: Cần có khả năng viết mã nguồn sạch sẽ (clean code), dễ đọc, và có khả năng mở rộng.
2.3. Kỹ năng Kiểm tra và Gỡ lỗi (Debugging)
Gỡ lỗi là một phần không thể tách rời của quá trình phát triển thuật toán.
- Kiểm thử: Tạo ra các test case điển hình và đặc biệt (ví dụ: biên, trường hợp rỗng, trường hợp xấu nhất) để kiểm tra tính đúng đắn của thuật toán.
- Gỡ lỗi hiệu quả: Sử dụng các công cụ gỡ lỗi (debugger) hoặc kỹ thuật in ra màn hình (print/log) một cách thông minh để theo dõi luồng dữ liệu và tìm ra lỗi logic.
3. Các Phương Pháp Tiếp Cận Giải Bài Toán NP-Khó
Phần cuối tài liệu đề cập đến một chủ đề nâng cao và quan trọng là các hướng tiếp cận để giải quyết các bài toán NP-khó (NP-hard). Đây là những bài toán mà hiện tại chưa có thuật toán đa thức (polynomial time, $O(N^k)$) nào được biết đến để tìm ra lời giải tối ưu.
3.1. Các Phương Pháp Giải Thuật Chính Xác
Đối với các bài toán có kích thước nhỏ hoặc các trường hợp cụ thể, vẫn có thể áp dụng các phương pháp chính xác để tìm ra lời giải tối ưu:
- Quy hoạch Động (Dynamic Programming – DP): Phương pháp này được sử dụng khi bài toán có cấu trúc con tối ưu và các bài toán con chồng chéo. DP cho phép tìm lời giải tối ưu bằng cách giải các bài toán con một lần và lưu trữ kết quả.
- Tìm kiếm Quay lui (Backtracking): Áp dụng cho các bài toán tìm kiếm tất cả các lời giải hoặc lời giải tối ưu bằng cách thử từng khả năng và quay lui khi không thỏa mãn.
- Tìm kiếm Nhánh và Cận (Branch and Bound): Một kỹ thuật tìm kiếm trong không gian trạng thái, đặc biệt hiệu quả cho các bài toán tối ưu. Nó sử dụng cận trên và cận dưới để loại bỏ nhanh chóng các nhánh không tiềm năng, giảm thiểu không gian tìm kiếm.
- Lập trình Tuyến tính/Số nguyên (Linear/Integer Programming): Sử dụng các mô hình toán học để biểu diễn bài toán và giải bằng các công cụ chuyên dụng (solver).
3.2. Các Phương Pháp Siêu Thuật Toán (Metaheuristics)
Khi bài toán quá lớn và không thể tìm lời giải chính xác trong thời gian chấp nhận được, các siêu thuật toán (Metaheuristics) là lựa chọn hàng đầu. Đây là các phương pháp tiệm cận, tìm kiếm lời giải tốt (good solution) thay vì lời giải tối ưu tuyệt đối.
- Thuật toán Di truyền/Tiến hóa (Genetic/Evolutionary Algorithms): Mô phỏng quá trình tiến hóa tự nhiên (chọn lọc, lai ghép, đột biến) để tìm kiếm không gian lời giải.
- Tìm kiếm Tabu (Tabu Search): Sử dụng bộ nhớ để ghi nhớ các bước đã đi qua (danh sách tabu) nhằm tránh lặp lại các vòng lặp tìm kiếm không hiệu quả, thúc đẩy việc khám phá các vùng mới của không gian lời giải.
- Mô phỏng Tôi luyện Thép (Simulated Annealing): Mô phỏng quá trình làm lạnh kim loại. Thuật toán đôi khi chấp nhận các bước di chuyển xấu hơn (nhưng với xác suất giảm dần theo thời gian) để thoát khỏi các cực tiểu cục bộ (local optima).
- Thuật toán Đàn kiến (Ant Colony Optimization – ACO): Mô phỏng hành vi tìm kiếm thức ăn của đàn kiến, sử dụng cơ chế pheromone để đánh dấu và củng cố các đường đi tốt.
3.3. Học Tăng Cường (Reinforcement Learning – RL)
Tài liệu giới thiệu Học Tăng Cường là một hướng tiếp cận hiện đại và mạnh mẽ, thuộc một trong ba nhánh chính của Học Máy, áp dụng cho các bài toán tối ưu có thể mô hình hóa dưới dạng một quá trình ra quyết định tuần tự.
- Mô hình: RL xây dựng một môi trường mô phỏng cho phép tác nhân (agent) tương tác thông qua một chuỗi các hành động (action).
- Hàm Q(s, a): Tác nhân rút kinh nghiệm và ra quyết định từng bước dựa trên Hàm Q(s, a), ước lượng độ tốt của hành động $a$ đối với trạng thái $s$.
- Phương pháp:
- Đối với không gian trạng thái nhỏ, có thể biểu diễn Q(s, a) dưới dạng bảng giá trị (value-based learning).
- Đối với không gian trạng thái rất lớn, áp dụng Học Tăng Cường Sâu (DRL), sử dụng mạng nơ-ron DNN để biểu diễn mối quan hệ giữa $s$, $a$, và $Q(s, a)$.
4. Cảm Nhận Cá Nhân và Đánh Giá Chi Tiết
Tài liệu “Thuật Toán Ứng Dụng” là một tài nguyên học tập xuất sắc, được xây dựng với tầm nhìn rõ ràng và tính thực tiễn cao, đặc biệt phù hợp với sinh viên ngành Công nghệ Thông tin. Cảm nhận cá nhân của tôi về tài liệu này được thể hiện qua các khía cạnh dưới đây.
4.1. Sự Kết hợp Hoàn hảo giữa Lý thuyết và Thực tiễn
Điểm mạnh lớn nhất của tài liệu là sự nhấn mạnh vào sự liên kết giữa tư duy thuật toán, cấu trúc dữ liệu, và kỹ năng lập trình. Tư duy thuật toán không chỉ là việc ghi nhớ công thức, mà là khả năng phân tích ràng buộc và đánh giá hiệu suất (độ phức tạp $O(\cdot)$). Việc tài liệu đề cập đến hệ thống chấm điểm ngay trong mô hình tổng quát cho thấy tính ứng dụng và sát với môi trường thi đấu lập trình (Competitive Programming) cũng như công nghiệp phần mềm, nơi hiệu suất là yếu tố sống còn.
4.2. Tính Toàn diện và Cập nhật của Nội dung
Tài liệu không chỉ giới hạn ở các thuật toán kinh điển mà còn mở rộng đến các chủ đề nâng cao và tiên tiến nhất trong tối ưu hóa.
- Khả năng mở rộng: Việc phân loại chi tiết các phương pháp giải bài toán NP-khó thành các phương pháp chính xác và siêu thuật toán (Metaheuristics) (như Thuật toán Di truyền, Tìm kiếm Tabu, Simulated Annealing, ACO) cung cấp một bản đồ tư duy đầy đủ. Điều này giúp người học biết rằng không phải bài toán nào cũng có lời giải tối ưu và đôi khi cần phải chấp nhận lời giải tiệm cận (approximate solution).
- Tính Hiện đại: Việc đưa Học Tăng Cường (RL) vào làm một hướng tiếp cận giải quyết bài toán NP-khó là một điểm nhấn hiện đại. RL và DRL (Deep Reinforcement Learning) đang là xu hướng mạnh mẽ trong việc giải quyết các bài toán tối ưu hóa phức tạp, đặc biệt là các vấn đề ra quyết định tuần tự (Sequential Decision Making). Điều này cho thấy tài liệu không chỉ dạy kiến thức cổ điển mà còn cập nhật những phương pháp nghiên cứu mới nhất.
4.3. Đánh giá về Cấu trúc Sư phạm
Mặc dù tài liệu chỉ là slide, cấu trúc của nó rất rõ ràng và logic: Bắt đầu từ Mô hình Tổng quát $\rightarrow$ Kỹ năng Cần rèn luyện $\rightarrow$ Các Dạng bài toán $\rightarrow$ Phương pháp Giải các bài toán khó. Trình tự này giúp người học xây dựng kiến thức theo từng bước vững chắc.
- Phần Kỹ năng: Việc tập trung vào kỹ năng phân tích đầu vào/đầu ra/ràng buộc là cực kỳ quan trọng. Đây là rào cản lớn nhất của người mới học thuật toán, khi họ thường lao vào code mà không đánh giá đúng độ phức tạp. Sự nhấn mạnh vào $N \le 10^5$ hay $N \le 10^3$ để lựa chọn thuật toán $O(N \log N)$ hay $O(N^2)$ là bài học thực tế không thể bỏ qua.
- Độ Sâu: Tài liệu đã liệt kê và giải thích ngắn gọn các thuật toán Metaheuristics như Tìm kiếm vùng lân cận linh hoạt (VNS) và Tìm kiếm vùng lân cận không gian lớn (LNS), cho thấy sự đầu tư về mặt nội dung để giới thiệu các kỹ thuật tối ưu hóa hiện đại.
4.4. Hạn chế và Triển vọng Phát triển
Là một bộ slide bài giảng, tài liệu này có mục tiêu là tóm tắt và định hướng. Do đó, nó không thể cung cấp chi tiết toàn bộ chứng minh toán học và triển khai mã nguồn đầy đủ của các thuật toán phức tạp như Quy hoạch Động hay các Metaheuristics.
- Hạn chế: Để thực sự nắm vững, người học cần phải tự tìm kiếm tài liệu bổ sung, tham khảo các sách chuyên sâu về Thiết kế và Phân tích Thuật toán và Lập trình Tuyến tính.
- Triển vọng: Với nền tảng kiến thức này, người học hoàn toàn có đủ khả năng để tham gia vào các lĩnh vực như Tối ưu hóa Vận hành (Operations Research), Phát triển Game/AI, và các lĩnh vực chuyên sâu hơn của Khoa học Dữ liệu và Học Máy, đặc biệt là sau khi đã làm quen với DRL.
Tóm lại, bộ tài liệu này là một kim chỉ nam có giá trị, định hình tư duy giải quyết vấn đề và trang bị kiến thức hiện đại về thuật toán ứng dụng. Nó là một điểm khởi đầu hoàn hảo, đòi hỏi sự chủ động rèn luyện kỹ năng lập trình và tư duy thuật toán từ phía người học để đạt được hiệu suất cao trong môi trường chuyên nghiệp.