Tải FREE sách Đồ Thị Và Các Thuật Toán PDF

Mục lục

Lưu ý quan trọng

Bên dưới đây mình có spoil 1 phần nội dung trong tài liệu để bạn tham khảo trước về nội dung tài liệu / Sách. Để xem được full nội dung thì bạn hãy nhấn vào nút “Link tải PDF” ở trên để tải bản đầy đủ về nhé

Tải FREE sách Đồ Thị Và Các Thuật Toán PDF

1. Tổng quan về Lý thuyết Đồ thị và Tính ứng dụng

Tóm tắt nội dung: Giá trị cốt lõi của Lý thuyết Đồ thị

Theo Lời nói đầu, Lý thuyết Đồ thị (LTDH) là một ngành khoa học có vai trò đặc biệt quan trọng. Giá trị của nó nằm ở khả năng mô tả hình học các vấn đề phức tạp, dài dòng thành mô hình trực quan và cô đọng⁴. LTDH đã gắn kết nhiều ngành khoa học lại với nhau thông qua các khái niệm được sinh ra từ thực tiễn⁵.

Cuốn sách đề cập đến nhiều khái niệm quan trọng, phản ánh trực tiếp các bài toán thực tế, bao gồm: đường đi, chu trình, tập ổn định, nhân, chu số, sắc số, duyệt đồ thị, đường đi ngắn nhất, tâm đồ thị, luồng vận tải, đồ thị phẳng, cây bao trùm, cây biểu thức, và cây mã tiền tố tối ưu⁶. Sự tồn tại của các thuật toán ngắn gọn và lý thú đã giúp giải quyết rất nhiều bài toán phức tạp trong thực tế⁷.

Cuốn sách được biên soạn dựa trên các bài giảng tại Trường Đại học Khoa học Tự nhiên – Đại học Quốc gia Hà Nội ⁸, cam kết trình bày chi tiết các thuật toán để người học có thể cài đặt dễ dàng ⁹, và có phần bài tập giúp người học tự kiểm tra kiến thức¹⁰.

Cảm nhận cá nhân: Sức mạnh của Mô hình hóa

Sự ra đời của Lý thuyết Đồ thị là một bước nhảy vọt trong tư duy toán học và khoa học máy tính. Sự cảm nhận sâu sắc nhất về LTDH chính là khả năng tóm lược sự tương tác của các đối tượng trong thế giới thực vào hai thành phần cơ bản: Đỉnh (Vertex) đại diện cho các đối tượng và Cạnh (Edge) đại diện cho mối quan hệ nhị nguyên giữa chúng¹¹.

Trong bối cảnh hiện đại, nơi dữ liệu và sự kết nối bùng nổ, mô hình đồ thị trở thành ngôn ngữ chung cho nhiều lĩnh vực¹². Ví dụ, trong lĩnh vực Logistic, bài toán tìm đường đi ngắn nhất là cốt lõi để tối ưu hóa chi phí và thời gian vận chuyển¹³. Trong Khoa học Máy tính, việc phân tích luồng vận tải (network flow) là cơ sở cho việc thiết kế mạng lưới viễn thông và truyền tải dữ liệu hiệu quả¹⁴. Trong lĩnh vực Kế hoạch/Quản lý dự án, cây bao trùm (Spanning Tree) và các thuật toán liên quan giúp xác định cấu trúc mạng lưới hiệu quả nhất với chi phí tối thiểu.

Lời nói đầu đã khéo léo định vị cuốn sách không chỉ là một tài liệu học thuật mà còn là một bộ công cụ giải quyết vấn đề. Việc giới thiệu một loạt các khái niệm chuyên sâu ngay từ đầu cho thấy phạm vi kiến thức mà cuốn sách hướng tới là rất rộng và chuyên nghiệp. Sự nhấn mạnh vào việc trình bày thuật toán chi tiết là một điểm cộng lớn, biến sách từ lý thuyết thuần túy sang tài liệu thực hành, đáp ứng nhu cầu của các ngành kỹ thuật và tin học ứng dụng.

2. Các Khái niệm Cơ bản và Phân loại Đồ thị

2.1. Định nghĩa Đồ thị và Ánh xạ kề

Tóm tắt nội dung

Đồ thị được định nghĩa hình thức bằng hai cách tương đương¹⁵:

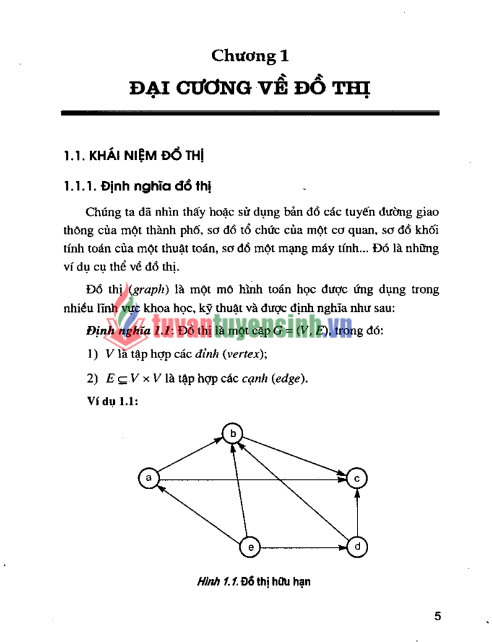
Định nghĩa 1.1 (Cặp đỉnh và cạnh): Đồ thị là một cặp $G=(V,E)$ trong đó $V$ là tập hợp các đỉnh (vertex), và $E \subseteq V \times V$ là tập hợp các cạnh (edge)¹⁶.
Định nghĩa 1.2 (Ánh xạ kề): Đồ thị là một cặp $G=(V,F)$, trong đó $V$ là tập hợp các đỉnh, và $F: V \rightarrow 2^{V}$ được gọi là ánh xạ kề¹⁷. $F(x)$ là tập hợp các đỉnh kề với đỉnh $x$. Sự tương đương được thể hiện: $\forall x,y \in V: (x,y) \in E \Leftrightarrow y \in F(x)$¹⁸.

Đồ thị là mô hình của các đối tượng (đỉnh) có quan hệ nhị nguyên (cạnh)¹⁹. Trên mặt phẳng, đỉnh được biểu diễn bằng các vòng tròn nhỏ, cạnh vô hướng là đoạn thẳng, cạnh có hướng là đường mũi tên²⁰. Cuốn sách chỉ xét các đồ thị hữu hạn, tức là tập đỉnh là hữu hạn²¹.

Cảm nhận cá nhân

Việc cung cấp hai định nghĩa chính thức cho đồ thị thể hiện sự chặt chẽ của tài liệu. Định nghĩa $G=(V,E)$ là định nghĩa tĩnh, mô tả cấu trúc bằng các tập hợp. Định nghĩa này rất phù hợp cho việc phân tích toán học và lý thuyết tập hợp.

Ngược lại, Định nghĩa $G=(V,F)$ sử dụng Ánh xạ kề (Adjacency mapping) lại mang tính động và hướng thuật toán cao hơn. Trong khoa học máy tính, đặc biệt khi biểu diễn đồ thị bằng danh sách kề (Adjacency List)²², định nghĩa này trực quan hơn rất nhiều. Ánh xạ $F(x)$ cung cấp danh sách tất cả các đỉnh mà ta có thể đi tới từ $x$ trong một bước duy nhất. Điều này là cốt lõi cho các thuật toán tìm kiếm như DFS (Depth-First Search) và BFS (Breadth-First Search), vốn là cơ sở của thuật toán duyệt đồ thị²³.

Đặc biệt, sự phân biệt giữa cặp đỉnh không sắp thứ tự (cạnh vô hướng) và cặp đỉnh có sắp thứ tự (cạnh có hướng) ²⁴ là nền tảng để phân loại đồ thị.

2.2. Phân loại và Đặc tính Đồ thị

Tóm tắt nội dung

Đồ thị được phân thành hai lớp chính dựa trên tính chất của cạnh:

Đồ thị vô hướng (Undirected Graph): Chỉ chứa các cạnh vô hướng²⁵.
Đồ thị có hướng (Directed Graph): Chỉ chứa các cạnh có hướng²⁶.

Một đồ thị vô hướng hiển nhiên có thể biểu diễn bằng một đồ thị có hướng bằng cách thay mỗi cạnh vô hướng bằng hai cạnh có hướng tương ứng (đi và về)²⁷.

Đồ thị đối xứng (Symmetric Graph): Đồ thị $G=(V,E)$ được gọi là đối xứng nếu: $\forall x,y \in V: (x,y) \in E \Leftrightarrow (y,x) \in E$²⁸. Các đồ thị vô hướng là đồ thị đối xứng²⁹.

Phân loại theo số cạnh nối hai đỉnh:

Đơn đồ thị (Simple Graph): Mỗi cặp đỉnh được nối với nhau bởi không quá một cạnh³⁰.
Đa đồ thị (Multigraph): Có những cặp đỉnh được nối với nhau nhiều hơn một cạnh³¹.

Cảm nhận cá nhân

Sự phân loại này là cơ sở để chọn thuật toán phù hợp. Trong thực tế, các mạng lưới giao thông hai chiều (đường phố) thường được mô hình hóa bằng đồ thị vô hướng/đối xứng³². Ngược lại, mạng lưới máy tính hoặc quy trình công việc có độ trễ hay chi phí khác nhau cho chiều đi và chiều về, hay các mối quan hệ một chiều (ví dụ: cấp bậc tổ chức) thì phải được mô hình hóa bằng đồ thị có hướng³³.

Đặc điểm đơn đồ thị cũng rất quan trọng. Trong nhiều bài toán lý thuyết, người ta thường mặc định xét đơn đồ thị để tránh sự phức tạp của việc có nhiều cạnh cùng nối hai đỉnh. Tuy nhiên, trong các bài toán thực tế về mạng lưới viễn thông, nơi có nhiều đường truyền song song giữa hai điểm, khái niệm đa đồ thị là cần thiết để mô hình hóa chính xác³⁴. Việc cuốn sách nhắc đến cả hai loại này cho thấy tính toàn diện trong việc giới thiệu các mô hình toán học cần thiết.

3. Các Đối tượng Cấu trúc Liên quan trong Đồ thị

3.1. Đường đi và Chu trình

Tóm tắt nội dung

Đường đi và chu trình là hai đối tượng động cơ bản nhất trong đồ thị:

Đường đi (Path): Là một dãy các đỉnh $<x_{1}, x_{2}, …, x_{k}>$ sao cho mỗi đỉnh (từ $x_{2}$ trở đi) kề với đỉnh ngay trước nó bằng một cạnh, tức là $\forall i=2, 3, …, k: (x_{i-1}, x_{i}) \in E$³⁵.
Độ dài: Là số cạnh của đường đi đó³⁶.
Đường đi đơn (Simple Path): Đường đi mà các đỉnh trên nó khác nhau từng đôi³⁷.
Chu trình (Cycle): Là một đường đi khép kín, tức là đỉnh cuối ($x_{k}$) trùng với đỉnh đầu ($x_{1}$)³⁸³⁸³⁸³⁸³⁸. Chu trình được ký hiệu là $[x_{1}, x_{2}, …, x_{k}]$ với $x_{1}=x_{k}$³⁹.
Chu trình đơn (Simple Cycle): Chu trình mà các đỉnh trên nó khác nhau từng đôi (trừ đỉnh đầu và đỉnh cuối trùng nhau)⁴⁰.
Đỉnh nút (Loop): Đỉnh kề với chính nó⁴¹.
Cạnh kề nhau: Hai cạnh có ít nhất một đỉnh chung⁴².

Cảm nhận cá nhân

Đường đi và chu trình không chỉ là định nghĩa hình thức mà còn đại diện cho hai nhóm bài toán lớn nhất của LTDH.

Đường đi là cơ sở cho các bài toán tối ưu hóa và tìm kiếm, như tìm đường đi ngắn nhất (Shortest Path) – một trong những thuật toán được nhắc đến ở Lời nói đầu⁴³.
Chu trình là cơ sở cho các bài toán về tính tuần hoàn và độ tin cậy của hệ thống. Trong mạng lưới, một chu trình có thể là một vòng lặp không mong muốn (gây tắc nghẽn), nhưng trong các hệ thống điện hoặc logic, nó có thể là một vòng phản hồi cần thiết.

Sự phân biệt giữa Đường đi đơn và đường đi không đơn là thiết yếu. Trong thực tế, khi tìm đường đi từ A đến B, ta luôn quan tâm đến đường đi đơn, vì việc đi qua cùng một điểm nhiều lần chỉ làm tăng độ dài (chi phí) mà không mang lại hiệu quả, trừ một số bài toán đặc biệt như bài toán người bán hàng (Travelling Salesman Problem).

3.2. Đồ thị con và Đồ thị riêng

Tóm tắt nội dung

Đồ thị con (Subgraph – $G’$): $G’ = (V’, E’)$ được gọi là đồ thị con của $G=(V,E)$ nếu $V’ \subseteq V$ và $E’$ là tập hợp tất cả các cạnh trong $E$ mà hai đỉnh của nó đều thuộc $V’$⁴⁴. Để xác định một đồ thị con, chỉ cần nêu tập đỉnh của nó⁴⁵.
Đồ thị riêng (Partial Graph – $G”$): $G” = (V, E”)$ được gọi là đồ thị riêng của $G=(V,E)$ nếu nó giữ nguyên tập đỉnh $V$ và $E” \subseteq E$ (bỏ bớt một số cạnh)⁴⁶⁴⁶⁴⁶⁴⁶.

Cảm nhận cá nhân

Hai khái niệm này rất quan trọng trong việc phân tích và cô lập vấn đề.

Đồ thị con cho phép chúng ta cô lập một phần của hệ thống (một nhóm thành phố, một cụm máy chủ) và phân tích mối quan hệ chỉ trong phạm vi đó. Điều này rất hữu ích khi hệ thống lớn quá mức để phân tích toàn bộ, cho phép áp dụng chiến lược chia để trị (Divide and Conquer).
Đồ thị riêng cho phép ta giữ nguyên toàn bộ các thành phần (đỉnh) nhưng xem xét ảnh hưởng của việc loại bỏ một số mối quan hệ (cạnh). Ví dụ, nếu một tuyến đường (cạnh) bị đóng, việc phân tích đồ thị riêng sẽ cho biết liệu vẫn còn đường đi giữa các điểm hay không. Khái niệm này là nền tảng cho việc xác định cây bao trùm (Spanning Tree) – là một đồ thị riêng không có chu trình, được nhắc đến ở Lời nói đầu⁴⁷.

3.3. Sự Đẳng hình của các Đồ thị

Tóm tắt nội dung

Đẳng hình (Isomorphism): Hai đồ thị $G_{1}=(V_{1},E_{1})$ và $G_{2}=(V_{2},E_{2})$ được gọi là đẳng hình nếu tồn tại một song ánh $S: V_{1} \rightarrow V_{2}$ bảo toàn các cạnh4848484848:$$\forall x,y \in V_{1}: (x,y) \in E_{1} \Leftrightarrow (S(x), S(y)) \in E_{2}$$
Về thực chất, hai đồ thị đẳng hình chỉ khác nhau về tên gọi của các đỉnh và cách biểu diễn bằng hình vẽ⁴⁹. Chúng ta thường không phân biệt hai đồ thị đẳng hình với nhau⁵⁰.

Cảm nhận cá nhân

Khái niệm đẳng hình là một trong những khái niệm lý thuyết quan trọng nhất. Nó cho phép các nhà khoa học và kỹ sư nhận ra rằng hai bài toán có vẻ ngoài khác nhau (ví dụ: sơ đồ mạch điện và bản đồ giao thông) lại có cùng một cấu trúc toán học cơ bản và có thể được giải quyết bằng cùng một thuật toán.

Việc không phân biệt các đồ thị đẳng hình với nhau ⁵¹ là một sự thừa nhận rằng cấu trúc quan hệ (Edges) mới là yếu tố cốt lõi, chứ không phải bản thân các đối tượng (Vertices) hay hình thức vẽ ra. Trong tin học, bài toán kiểm tra tính đẳng hình của hai đồ thị (Graph Isomorphism Problem) là một trong những bài toán thách thức và chưa được chứng minh thuộc lớp P hay NP-complete, chứng tỏ độ phức tạp và tầm quan trọng của nó.

4. Các Cách Biểu diễn Đồ thị trong Máy tính

4.1. Biểu diễn bằng Ma trận kề

Tóm tắt nội dung

Đồ thị $G=(V,E)$ với $n$ đỉnh (được đánh số $1, 2, …, n$) có thể được biểu diễn bằng một ma trận vuông $A_{n \times n}$ được gọi là ma trận kề⁵².

Cấu trúc: Phần tử $A[i, j] = d$, trong đó $d$ là số cạnh nối đỉnh $i$ với đỉnh $j$ trong đồ thị $G$⁵³.
Đặc điểm: Đồ thị $G$ là đối xứng khi và chỉ khi ma trận kề $A$ là đối xứng ($A[i, j] = A[j, i]$)⁵⁴.

Định lý về số lượng đường đi:

Định lý 1.1: Phần tử ở hàng $i$ và cột $j$ của ma trận luỹ thừa $A^{k}$ là số các đường đi khác nhau có độ dài $k$ nối đỉnh $i$ với đỉnh $j$ trong đồ thị $G$⁵⁵.

Chứng minh Định lý 1.1:

Việc chứng minh định lý được thực hiện bằng phương pháp quy nạp theo độ dài $k$ của đường đi⁵⁶:

Trường hợp cơ sở $k=1$: Theo định nghĩa của ma trận kề, $A[i, j]$ là số cạnh nối $i$ với $j$. Một cạnh chính là một đường đi có độ dài $1$. Do đó, Định lý đúng với $k=1$⁵⁷.
Bước quy nạp $(k) \Rightarrow (k+1)$: Giả sử Định lý đúng với $k$ (tức là $A^{k}[i, j]$ là số đường đi độ dài $k$ từ $i$ đến $j$)⁵⁸⁵⁸⁵⁸.
- Ta cần tính ma trận $C = A^{k+1} = A^{k} \cdot A$⁵⁹.
- Phần tử $c_{i, j}$ của $C$ được tính bằng công thức nhân ma trận:$$c_{i, j} = \sum_{q=1}^{n} b_{i, q} a_{q, j}$$Trong đó $A^k = [b_{i, j}]$ và $A = [a_{i, j}]$⁶⁰⁶⁰⁶⁰⁶⁰⁶⁰⁶⁰⁶⁰⁶⁰.
- Theo giả thiết quy nạp, $b_{i, q}$ là số đường đi từ đỉnh $i$ đến đỉnh $q$ có độ dài $k$⁶¹⁶¹.
- $a_{q, j}$ là số cạnh nối đỉnh $q$ với đỉnh $j$⁶².
- Mỗi đường đi độ dài $k$ từ $i$ đến $q$, khi được nối thêm một cạnh từ $q$ đến $j$, sẽ tạo thành một đường đi từ $i$ đến $j$ có độ dài $k+1$ đi qua đỉnh $q$⁶³. Số lượng các đường đi này là $b_{i, q} \cdot a_{q, j}$⁶⁴.
- Bằng cách lấy tổng $\sum_{q=1}^{n}$ qua tất cả các đỉnh trung gian $q$, ta sẽ có tất cả các đường đi từ $i$ đến $j$ với độ dài $k+1$⁶⁵. Định lý được chứng minh.

Cảm nhận cá nhân

Biểu diễn bằng Ma trận kề là một trong những phương pháp mang tính toán học và hình thức cao nhất. Ưu điểm của nó là sự đơn giản và dễ dàng cho các phép tính đại số tuyến tính. Nhược điểm là tốn kém về không gian nhớ ($\mathcal{O}(n^2)$)⁶⁶, đặc biệt đối với các đồ thị thưa (ít cạnh).

Tuy nhiên, Định lý 1.1 là một ví dụ tuyệt vời về sự kết hợp giữa Lý thuyết Đồ thị và Đại số Tuyến tính. Định lý này mang lại một công cụ tính toán mạnh mẽ và thanh lịch: để tìm số đường đi độ dài $k$, chỉ cần nâng ma trận kề lên luỹ thừa $k$. Điều này rất hữu ích trong việc phân tích tính kết nối và độ tin cậy của mạng lưới.

Việc phân tích chứng minh Định lý 1.1 bằng quy nạp cho thấy tính chặt chẽ của tài liệu. Quy tắc nhân ma trận được diễn giải lại dưới góc độ đồ thị: Tích ma trận là sự tổng hợp các đường đi qua một đỉnh trung gian $q$⁶⁷⁶⁷⁶⁷⁶⁷. Điều này củng cố sự hiểu biết rằng ma trận kề không chỉ là một bảng số mà là một mô tả hoàn chỉnh về cấu trúc kết nối của đồ thị.

4.2. Biểu diễn bằng Danh sách kề

Tóm tắt nội dung

Danh sách kề (Adjacency List): Với mỗi đỉnh của đồ thị, ta xây dựng một danh sách móc nối (Linked List) chứa các đỉnh kề với đỉnh đó⁶⁸.
Một đồ thị được biểu diễn bằng một mảng các danh sách kề⁶⁹.

Cảm nhận cá nhân

Biểu diễn bằng Danh sách kề là phương pháp được ưu tiên trong hầu hết các ứng dụng lập trình thực tế, đặc biệt là trong các thuật toán tìm kiếm và duyệt đồ thị, cũng như các đồ thị thưa (sparse graphs).

Trong khi Ma trận kề tốn $\mathcal{O}(n^2)$ bộ nhớ, Danh sách kề chỉ tốn $\mathcal{O}(n + m)$ bộ nhớ (với $n$ là số đỉnh và $m$ là số cạnh)⁷⁰. Đối với các đồ thị lớn và thưa, sự tiết kiệm bộ nhớ là rất đáng kể. Hơn nữa, việc duyệt các đỉnh kề (tìm kiếm các đỉnh trong $F(x)$ theo Định nghĩa 1.2) trong danh sách kề là trực tiếp và hiệu quả hơn.

Sự đối lập giữa hai phương pháp biểu diễn này (Ma trận kề cho tính toán đại số vs. Danh sách kề cho thao tác thuật toán) là một bài học quan trọng trong khoa học máy tính: Không có một cấu trúc dữ liệu nào là tối ưu cho mọi trường hợp, mà phải chọn cấu trúc phù hợp với mục tiêu giải quyết bài toán (ví dụ: cần tính số đường đi độ dài $k$ thì dùng Ma trận, cần duyệt đồ thị thì dùng Danh sách).

5. Kết luận Chung về Tài liệu và Triết lý Học tập

Cuốn sách “ĐỒ THỊ và CÁC THUẬT TOÁN” là một tài liệu học thuật chất lượng cao, cung cấp một nền tảng vững chắc về LTDH. Nó không chỉ là tập hợp các định nghĩa toán học mà còn là một khóa học về tư duy mô hình hóa và phân tích thuật toán.

Tính Hình thức và Chặt chẽ: Tài liệu giới thiệu các khái niệm (Đồ thị, Ánh xạ kề, Đường đi, Chu trình, Đẳng hình) bằng các Định nghĩa Toán học chặt chẽ⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹⁷¹. Việc đưa ra chứng minh cho Định lý 1.1 về lũy thừa ma trận kề ⁷² là một minh chứng cho sự chặt chẽ này.
Tính Ứng dụng và Thuật toán: Ngay từ Lời nói đầu, cuốn sách đã nhấn mạnh vai trò của các thuật toán (đường đi ngắn nhất, luồng vận tải, cây bao trùm) trong việc giải quyết các vấn đề thực tiễn⁷³. Điều này định hướng cho người học về mục tiêu cuối cùng: không chỉ hiểu lý thuyết mà còn phải biết cách cài đặt và áp dụng thuật toán⁷⁴.
Tầm quan trọng trong Tin học: Hai phương pháp biểu diễn đồ thị trong máy tính (Ma trận kề và Danh sách kề) là kiến thức nền tảng bắt buộc đối với bất kỳ ai theo đuổi ngành Tin học. Sự đối chiếu giữa chúng là bài học đầu tiên về việc lựa chọn cấu trúc dữ liệu tối ưu dựa trên yêu cầu bộ nhớ và hiệu suất thuật toán.

Cuốn sách, qua những chương đầu tiên, đã thành công trong việc tạo ra một khung tham chiếu vững chắc cho việc nghiên cứu sâu hơn về các thuật toán đồ thị phức tạp hơn. Việc học tập theo tài liệu này không chỉ trang bị kiến thức về một ngành toán học mà còn rèn luyện tư duy phân tích, mô hình hóa, và giải quyết vấn đề bằng công cụ Tin học, những kỹ năng then chốt của kỷ nguyên số.